La loi de Poisson est une distribution de probabilité discrète, qui exprime la probabilité qu’un nombre k d’événements se produisent dans un temps ou un espace fixe si ces événements se produisent avec un taux moyen connu. Ces évènements sont indépendants du temps ou de l’espace depuis le dernier événement.
Définition de la loi de Poisson
La loi de Poisson porte le nom de Siméon Dennis Poisson (1781-1840), un Français qui a développé cette distribution sur la base d’études menées dans la dernière partie de sa vie.
La distribution de Poisson est une distribution de probabilité discrète et est utilisée pour décrire des processus qui peuvent être décrits par une variable aléatoire discrète. Elle décrit des situations dans lesquelles les clients arrivent indépendamment les uns des autres pendant un certain intervalle de temps et le nombre d’arrivées dépend de l’ampleur de l’intervalle.
Principes de la loi de Poisson
Une variable aléatoire X suit une distribution de Poisson si elle peut prendre les valeurs entières 0, 1, 2, …, n, …, avec des probabilités :
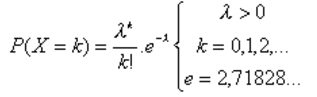
Dans cette distribution, il est nécessaire d’observer :
- Elle ne dépend que d’un seul paramètre.
- Sa moyenne et sa variance sont
![]()
- C’est une bonne approximation de la binomiale lorsque n est grand et p est petit :
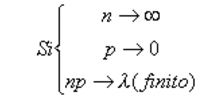
puis
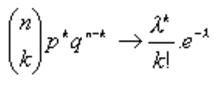
En général, si n>50 et p<0,1 ou n.p<5, la distribution de Poisson est une bonne approximation de la distribution Binomiale.
- La distribution de Poisson présente une légère asymétrie vers la gauche. Lorsque n tend vers l’infini, il tend à être symétrique (distribution normale).
Conditions nécessaires pour l’application de la loi de Poisson
La distribution de Poisson, comme nous l’avons souligné, fait référence à certains processus qui peuvent être décrits par une variable aléatoire discrète. La lettre X représente généralement cette variable et peut également prendre des valeurs entières (0,1,2,3 etc.). Nous utilisons la lettre majuscule X pour représenter la variable aléatoire et la minuscule x pour désigner une valeur spécifique que la majuscule X peut prendre. La probabilité d’exactement x occurrences dans une distribution de Poisson est calculée par la formule :
P(x) = l x * e-l / x !
l x = Lambda (nombre moyen d’occurrences par intervalle de temps) élevé à la puissance x.
e-l = e= 2.71828 élevé à la puissance de lambda négatif.
x ! = x factoriel.
Domaine d’application de la loi de Poisson
Parmi les processus qui peuvent être décrits à l’aide de la distribution de probabilité de Poisson figurent la distribution des appels téléphoniques qui arrivent à un standard téléphonique, la demande (les besoins) de services dans un établissement de soins de santé par les patients, les arrivées de camions et de voitures au poste de péage et le nombre d’accidents à une intersection. Ces exemples cités ont un élément en commun. Ils peuvent être décrits par une variable aléatoire discrète qui prend des valeurs entières.
La distribution de Poisson joue un rôle important en complétant la distribution exponentielle dans la théorie des files d’attente ou le modèle de la ligne d’attente.
Résumé de la loi de Poisson
La distribution de Poisson sert à décrire des processus par une variable aléatoire discrète qui prend des valeurs entières (0,1,2,3,4,5 et ainsi de suite).











